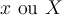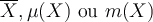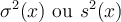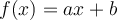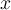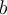Références et lectures conseillées

Lectures conseillées
Falissard, B. (2001).
Mesurer la subjectivité en santé : Perspective méthodologique et statistique
. Paris : Masson.
Howell, D.C. (2008),
Méthodes Statistiques en Sciences Humaines
(6e éd). Paris : De Boeck.
Huteau, M., & Lautrey, J. (1999).
Évaluer l'intelligence
. Paris : Presses Universitaires de France.
Laveault, D., & Grégoire, J. (2002).
Introduction aux théories des tests en Psychologie et en Sciences de l'Education
(2e éd.). Bruxelles : De Boeck.
Reuchlin, M. (1998).
Précis de statistique
(7e éd.). Paris : Presses Universitaires de France
Références utilisées et/ou citées dans ce site
- Ancelle, T. (2002). Statistique épidémiologie. Paris : Editions Maloine.
- Aron, A., Aron, E.N., & Coups, E.J. (2005). Statistics for the behavioral and social sciences: A brief course. Upper Saddle River, NJ: Pearson Prentice Hall.
- Barbut, M., & Monjardet, B. (1970a). Ordre et classification, algèbre et combinatoire. Tome 1. Hachette Université.
- Barbut, M., & Monjardet, B. (1970b). Ordre et classification, algèbre et combinatoire. Tome 2. Hachette Université.
- Beaufils, B. (1991). Étude de statistiques descriptives. Vanves : CNED.
- Bergson, H. (1939). Matière et mémoire. Essai sur la relation du corps à l'esprit. Paris : Presses Universitaires de France.
- Bollen, K. A. (2002). Latent variables in psychology and the social sciences. Annual Review of Psychology, 53, 605-634.
-
Canguilhem, G. (1958).
Qu'est-ce que la psychologie
?
Revue de Métaphysique et de Morale, 1
, 12-25.
- Cattell, J. M. (1890). Mental tests andmeasurements.Mind, 15, 373-380.
- Cowppli-Bony, P., Fabrigoule, C., Letenneur,L., Ritchie, K., Alpérovitch, A., Dartigues, J. F., & Dubois, B.(2005). Letest des 5 mots : validité dans la détection de la maladie d'Alzheimer dans la population générale. Revue Neurologique, 161, 1205-1212.
- Costa, P. T. Jr., & McCrae, R. R. (2007). NEO PI-R : Inventaire de personnalité-révisé, manuel (J.-P. Rolland, adaptation française). Paris : Hogrefe.
- Cronbach, L.J. (1990). Essentials of psychological testing (5th ed.). New York: HarperCollinsPublishers.
- Cronbach, L. J., & Meehl, P. H. (1955). Construct validity in psychological tests. Psychological Bulletin, 52, 281-302.
- Degraeve, B. (2022). Statistiques en psychologie et neuropsychologie. Dunod.
- Gigerenzer, G., Swijtink, Z., Porter, T., Daston, L., Beatty, J., & Krüger, L. (1989). The empire of chance: How probability changed science and everyday life. Cambridge: Cambridge University Press.
- Guillevic, C., & Vautier, S. (2005). Diagnostic et tests psychologiques (2e ed.). Paris : Armand Colin.
- Likert, R, Roslow, S., & Murphy, G. (1993). A simple and reliable method for scoring the Thurstone attitude sclale. Personnel Psychology, 46, 689-690.
- Maraun, M. D. (1998). Measurement as a normative practice: Implications of Wittgenstein's philosophy for measurement in psychology. Theory & Psychology, 8, 435-462.
- Martin, L., & Baillargeon, G. (1989). Statistiqueappliquée à la psychologie (2e éd.). Trois-Rivières, Qc : Les Editions SMG.
- Michell, J. (1990). An introduction to the logic of psychological measurement. Hillsdale, NJ: Lawrence Erlbaum Associates.
- Michell, J. (2000). Normal science, pathologicalscience and psychometrics. Theory & Psychology, 10, 639-667.
- Michell, J. (2003). The quantitative imperative: Positivism, naïve realism, and the place of qualitative methods in psychology. Theory & Psychology, 13, 5-31.
- Michell, J. (2005). The logic of measurement: A realist overview. Measurement: Interdisciplinarity Research andPerspectives, 38, 285-294.
- Monod, J. (1970). Le hasard et la nécessité. Essai sur la philosophie naturelle de la biologie moderne. Paris : Seuil.
- Pichot, P. (1949). Les tests mentaux en psychiatrie, I. Instruments et méthodes. Paris : PUF.
- Pichot, P. (1967). Les tests mentaux (6e édition). Paris : PUF.
- Reuchlin, M. (1969). Les méthodes en psychologie. Paris : PUF.
- Reuchlin,M. (1991). Les différences individuelles à l’école. Paris : Presses Universitaires de France.
- Salsburg, D. (2001). The lady tasting tea: How statistics revolutionized science in the twentieth century. New York, Henry Holt Books.
- Saunders, J.B., Aasland, O.G., Babor, T.F., de la Fuente, J.R., & Grant ,M. (1993). Development of the Alcohol Use Disorders Identification Test (AUDIT): WHO Collaborative Project on Early Detection of Persons with Harmful Alcohol Consumption-II. Addiction, 88, 791-804.
- Snow, R.E., & Lohman,D.F. (1984).Toward a theory of cognitive aptitude for learning from instructions.Journal of EducationalPsychology, 76, 347-376.
-
Spielberger, C. D., Gorsuch, R. L., Lushene, R., Vagg, P. R., & Jacobs, G. A. (1993).
Manuel de l'inventaire d'anxiété état-trait forme Y
(STAI-Y)
(M. Bruchon-Schweitzer & I. Paulhan, adapt. française). Paris : Editions du Centre de Psychologie Appliquée.
- Steyer, R. (1989). Models of classical psychometric test theory as stochastic measurement models: Representation, uniqueness, meaningfulness, identifiability, and testability. Methodika, 3, 25-60.
- Stevens, S. S. (1946). On the theory of scales of measurement. Science, 103,667-680.
- Tabachnik, B. G., & Fidell, L. S. (2001). Using multivariate statistics(4th ed.). Needham Heights, MA: Allyn and Bacon.
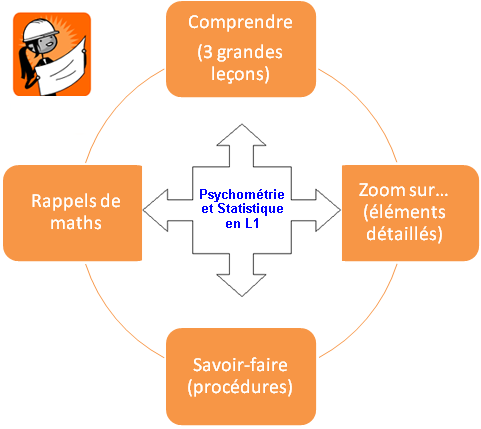

 Cette première grande leçon introduit la psychométrie et la statistique dans la perspective historique du développement de la psychologie scientifique à partir du XIX
e
siècle, afin de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques, et techniques de ces matières. Ces enjeux comprennent en particulier l'établissement de grandeurs mesurables et la mise au point de méthodes objectives pour l'étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette première grande leçon introduit la psychométrie et la statistique dans la perspective historique du développement de la psychologie scientifique à partir du XIX
e
siècle, afin de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques, et techniques de ces matières. Ces enjeux comprennent en particulier l'établissement de grandeurs mesurables et la mise au point de méthodes objectives pour l'étude de la variabilité induite expérimentalement ou observée en condition naturelle.
 Cette grande leçon développe la problématique de la mesure en psychologie dans une perspective épistémologique et historique. Il s'agit de poser le problème de l'observation objective et quantitative du comportement d'une part, et le problème de l'interprétation des données comme des variables théoriques d'autre part.
Cette grande leçon développe la problématique de la mesure en psychologie dans une perspective épistémologique et historique. Il s'agit de poser le problème de l'observation objective et quantitative du comportement d'une part, et le problème de l'interprétation des données comme des variables théoriques d'autre part. Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au 
 Objectifs : Définir le concept d'échelle de mesure et donner les éléments critiques nécessaires à son utilisation.
Objectifs : Définir le concept d'échelle de mesure et donner les éléments critiques nécessaires à son utilisation.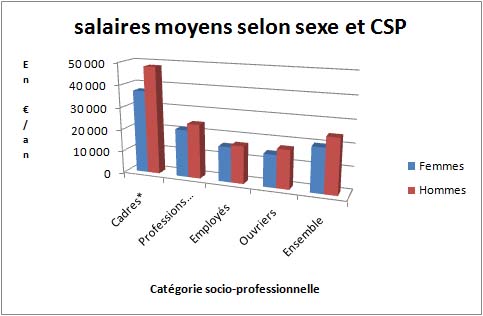 Variables, valeurs et modalités" et soit
Variables, valeurs et modalités" et soit 
 Objectifs : Illustrer avec une vidéo la notion de variables couramment utilisés en psychologie.
Objectifs : Illustrer avec une vidéo la notion de variables couramment utilisés en psychologie.